9592. Concatenation of two
palindromes
Find the number
of ways to construct a string of length n
using k Latin letters (the size of
the alphabet is k) as the concatenation
of two nonempty palindromes.
Input. Two positive integers n and k (1 ≤ n ≤ 105, 1 ≤ k ≤ 26).
Output. Print the number of ways to construct the
given string. Print the answer modulo 109 + 7.
Explanation. In the first test case the
string of length 4 using one letter (à for
example) can be constructed in three ways: a + aaa, aa + aa, aaa + a.
|
Sample
input 1 |
Sample
output 1 |
|
4 1 |
3 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
3 2 |
8 |
SOLUTION
exponentiation +
combinatorics
Algorithm analysis
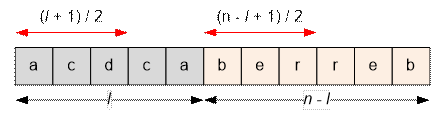
Let us represent
a string of length n as the
concatenation of two non-empty palindromes of lengths l and n – l.
Consider a
palindrome of length l. Since a
palindrome reads the same from left to right and from right to left, its second
half is completely determined by its first half. Therefore, it is sufficient to
choose arbitrarily only the first (l + 1) / 2 characters, each of which can be any of the k letters of the alphabet. The remaining
characters are then uniquely determined so that the string forms a palindrome.
Thus, the total
number of palindromes of length l is k(l+1)/2.
![]()
![]()
Similarly, for a
palindrome of length n – l, its second half is
completely determined by its first half. Therefore, the first (n – l + 1) / 2 characters can be chosen arbitrarily, with each of
them selected from the k letters of the
alphabet, while the remaining characters are uniquely determined by the
palindrome property.
Consequently, the
number of palindromes of length n – l is k(n-l+1)/2.
Constructing the concatenation of two
palindromes with lengths l and n – l can
be done in
k(l+1)/2 * k(n-l+1)/2
ways. Since neither of the palindromes should
be empty, then 1 ≤ l ≤ n – 1. The total number of possible palindromes is
![]()
All operations should be carried out modulo
109 + 7.
Example
Consider the second example, in which the
length of the string is 3 and the alphabet consists of two letters. Let these
letters be a and b.
·
Palindromes
of length 1: a and b.
·
Palindromes
of length 2: aa and bb.
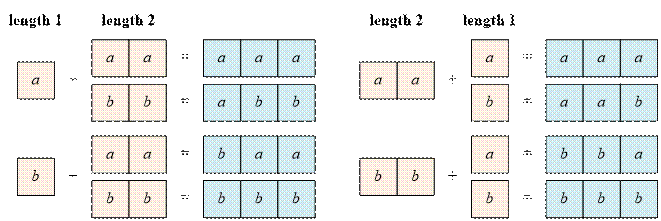
Thus, there are exactly 8 desired strings
of length 3:
Algorithm implementation
The computations are performed modulo 109 + 7. Let’s
define the modulo MOD.
#define MOD
1000000007
The powmod function computes the value of xn mod m.
long long
powmod(long long x, long long n, long long m)
{
if (n ==
0) return 1;
if (n % 2
== 0) return powmod((x * x) % m, n / 2,
m);
return (x *
powmod(x, n - 1, m)) % m;
}
The main part of the program. Read the input data.
scanf("%d %d",
&n, &k);
Compute the answer res using the formula.
res = 0;
for (l = 1; l < n; l++)
res = (res +
powmod(k, (l + 1) / 2, MOD) *
powmod(k, (n - l + 1) / 2, MOD)) % MOD;
Print the answer.
printf("%lld\n",
res);
Java implementation
import java.util.*;
public class Main
{
public final static long MOD = 1000000007;
static long PowMod(long x, long n, long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long k = con.nextLong();
long res = 0;
for (long l = 1; l < n; l++)
res = (res + PowMod(k, (l + 1) / 2, MOD) *
PowMod(k, (n - l + 1) / 2, MOD)) % MOD;
System.out.println(res);
con.close();
}
}
Python implementation
The computations are performed modulo 109 + 7. Let’s
define the modulo mod.
mod = 10 ** 9 + 7
Read the input data.
n, k = map(int, input().split())
Compute the answer res using the
formula.
res = 0;
for l in range(1,n):
res = (res + pow(k, (l + 1) // 2, mod)
*
pow(k, (n - l + 1) // 2, mod)) % mod;
Print the answer.
print(res)